位移、速度、加速度

位置矢量（位矢）

建立直角坐标系后，物体的位置可用坐标 $A(x, y, z)$ 表示。
向量 $\vec{r} = \overrightarrow{OA}$ 就称为位置矢量（位矢），也记为：
$\vec{r} = xi + yj + zk$
表示点 $(x, y, z)$ 的位置。

运动方程

原点坐标 $x, y, z$ 随时间的变化关系，将消掉时间 $t$ 即可。

例题

已知质点的运动学方程为：
$\vec{r} = 4t^2i + (2t + 3)j$
则质点的运动方程为：

$x = 4t^2$
$y = 2t + 3$

通过 $t = \frac{y - 3}{2}$ 代入第一个方程，得到：
$x = 4 \left( \frac{y - 3}{2} \right)^2$
化简得到：
$x = (y - 3)^2$

速度与速率

平均速度 $\vec{v} = \frac{\Delta \vec{r}}{\Delta t}$，平均速率是路程除以时间 $v = \frac{\Delta s}{\Delta t}$。
瞬时速度就是对每个坐标分量求导：
$$
\vec{v} = \frac{d \vec{r}}{dt} = \frac{dx}{dt} \vec{i} + \frac{dy}{dt} \vec{j} + \frac{dz}{dt} \vec{k}
$$
瞬时速率是瞬时速度的大小：
$$
v = \left| \frac{d \vec{r}}{dt} \right| = \frac{ds}{dt} = \sqrt{\left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 + \left( \frac{dz}{dt} \right)^2}
$$

注意

不能写成 $\frac{dr}{dt}$ 或 $\frac{d | \vec{r} |}{dt}$。

$|\mathrm{d} \vec{r}| = \mathrm{d}s$ 是正确的。

例题

运动质点在某瞬时位于矢径 $\vec{r} = (x, y)$ 的端点处，其速度大小为：
$$
\sqrt{\left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2}
$$

题目：

已知一质点在 $Oxy$ 平面内运动，运动学方程为 $x = 2t$，$y = 19 - 2t^2$，则在第 2 秒内质点的平均速度大小为 $2\sqrt{10} \ \mathrm{m/s}$，第 2 秒末的瞬时速度大小为 $2\sqrt{17} \ \mathrm{m/s}$。

加速度

平均加速度 $\vec{a} = \frac{\Delta \vec{v}}{\Delta t}$
瞬时加速度就是对每个速度分量求导：
$$
\vec{a} = \frac{d\vec{v}}{dt} = \frac{dv_x}{dt} \hat{i} + \frac{dv_y}{dt} \hat{j} + \frac{dv_z}{dt} \hat{k}
$$
注意：加速度与速度同号为加速，异号为减速，而不是正数加速，负数减速

位移、速度、加速度的互求

$v = \frac{dx}{dt}$，$a = \frac{dv}{dt}$
$v = v_0 + \int_0^t a , dt$，$x = x_0 + \int_0^t v , dt$
示意图：
- 坐标 $(x, y, z)$ 与速度 $(v_x, v_y, v_z)$ 之间可以通过求导和积分互求。
- 同样，速度 $(v_x, v_y, v_z)$ 与加速度 $(a_x, a_y, a_z)$ 也可以通过求导和积分互求。

圆周运动的参数

切向与法向加速度
- 加速度可以沿速度方向分解
- 与速度方向平行的称为切向加速度，改变速度的大小，$a_t = \frac{dv}{dt}$
- 与速度方向垂直的称为法向加速度，改变速度的方向，$a_n = \frac{v^2}{\rho}$
- 其中 $\rho$ 为曲率半径，若为圆周运动则为半径

【例】在半径为 $R$ 的圆周上运动的质点，其速度与时间关系为 $v = ct^2$，从 $0$ 时刻到 $t$ 时刻，质点走过的路程为 $s = \frac{1}{3}ct^3$；$t$ 时刻质点的切向加速度为 $a_t = 2ct$，法向加速度为 $a_n = \frac{c^2t^4}{R}$，总加速度的大小为
$$
a = \sqrt{(2ct)^2 + \left(\frac{c^2t^4}{R}\right)^2}
$$

圆周运动参数的互求

$\omega = \frac{d\theta}{dt}$，$\alpha = \frac{d\omega}{dt}$
$\omega = \omega_0 + \int_0^t \alpha , dt$，$\theta = \theta_0 + \int_0^t \omega , dt$
示意图：
- 角位移 $(\theta)$ 与角速度 $(\omega)$ 之间可以通过求导和积分互求。
- 同样，角速度 $(\omega)$ 与角加速度 $(\alpha)$ 也可以通过求导和积分互求。

角量与线量的关系

线速度 $v = \omega R$
法向加速度 $a_n = \frac{v^2}{R} = \omega^2 R$
切向加速度 $a_t = \frac{dv}{dt} = \alpha R$

【例】一质点从静止出发，沿半径为 $R=1$ 的圆周运动，角加速度 $\alpha = 12t^2 - 6t$，则质点的角速度 $\omega = 4t^3 - 3t^2$，切向加速度 $a_t = 12t^2 - 6t$，法向加速度 $a_n = (4t^3 - 3t^2)^2$，总加速度为 $a = \sqrt{(12t^2 - 6t)^2 + (4t^3 - 3t^2)^2}$。

计算：

$$
\omega = \int_0^6 (12t^2 - 6t) , dt = 4t^3 - 3t^2
$$

相对运动

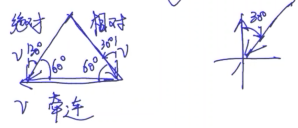
若相对只有平动，则位移、速度、加速度都满足：
- A的实际（绝对）= A相对B（相对）+ B的实际（牵连）

【例】某人骑自行车以速率v向西行驶，今有风以相同速率从北偏东30°方向吹来，试问人感到风从哪个方向吹来？

(A)北偏东30
(B)南偏东30°
©北偏西30° True
(D)西偏南30°